Skip to contents

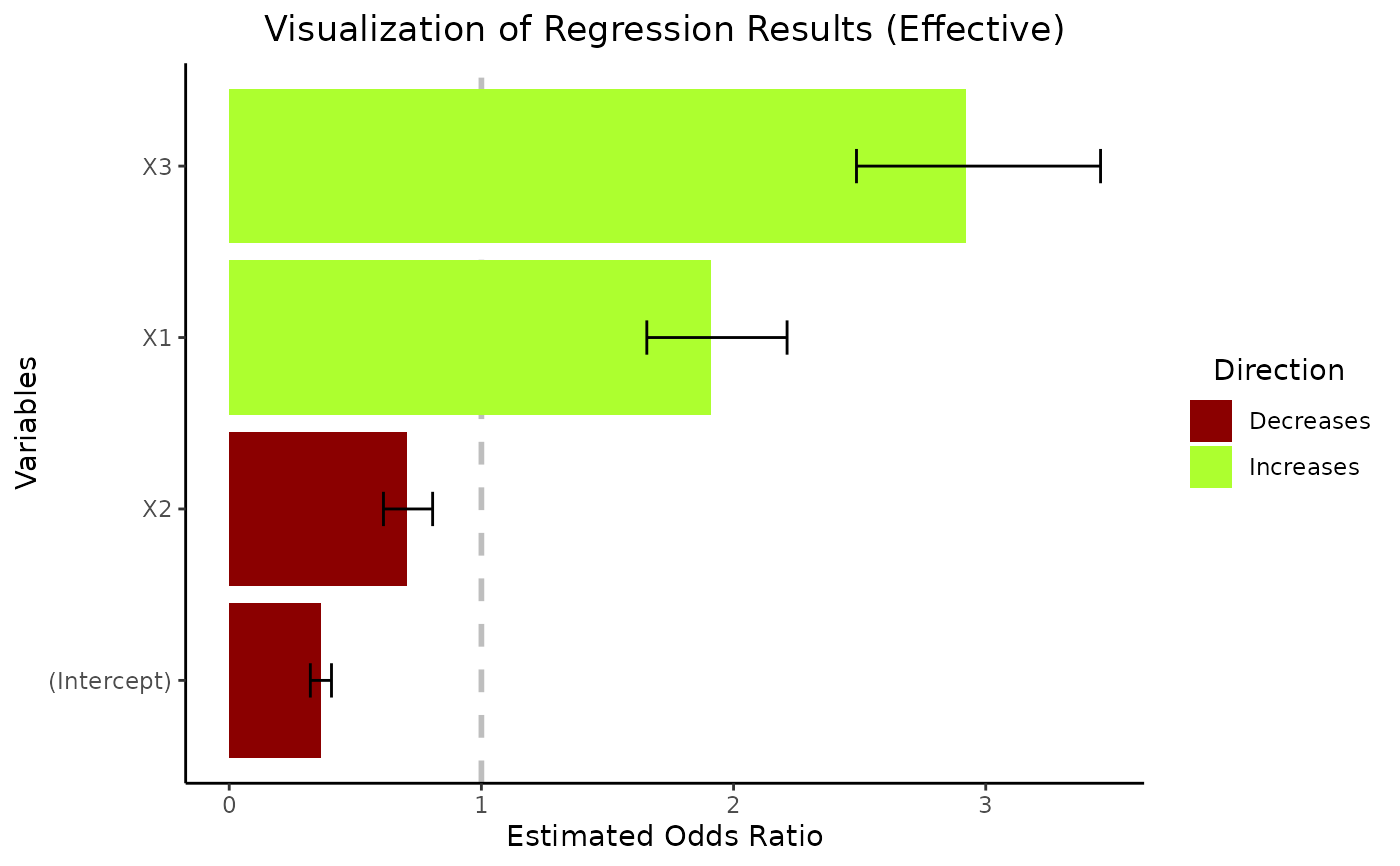
Visualize Regression Coefficients Within the Context of Empirical Data

vis_reg.Rd

Typically, regression coefficients for continuous variables are interpreted on a per-unit basis and compared against coefficients for categorical variables. However, this method of interpretation is flawed as it overlooks the distribution of empirical data. This visualization tool provides a more nuanced understanding of the regression model's dynamics, illustrating not only the immediate effect of a unit change but also the broader implications of larger shifts such as interquartile changes.

Usage

vis_reg(object, ...)

Arguments

object

A fitted model object, expected to be one of the following classes:

  • lm : Linear Models.

  • glm lm : Generalized Linear Models.

  • elnet glmnet : Regularized Linear Models.

  • lognet glmnet : Regularized Logistic Models.

  • fixedLassoInf : Inference for the lassso for the linear models.

  • fixedLogitLassoInf : Inference for the lassso for the logistic models.

...

Additional parameters.Please refer to details.

Value

A list with the following components:

  • $PerUnitVis: A ggplot object that visualizes regression coefficients on a per-unit basis

  • $RealizedEffectVis: A ggplot object that visualizes regression coefficients on a basis of realized effect calculation.

  • $SidebySide: A grob object containing both visualizations side-by-side.

Details

The following additional arguments can be passed:

  • CI: A logical value indicating whether to include Confidence Intervals.

    • The default is FALSE.

    • For fixedLassoInf or fixedLogitLassoInf classes it is set to TRUE.

    • confint() is used to generate CIs for the lm and glm lm classes.

    • If CIs are desired for the regularized models, please, fit your model using fixedLassoInf()function from theselectiveInferencepackage following the steps outlined in the documentation for this package and pass the object of classfixedLassoInforfixedLogitLassoInf`.

  • x_data_orig: Original non-centered and non-scaled model matrix without intercept.

    • Please, pass the model matrix when CIs desired for fixedLassoInf and/or fixedLogitLassoInf object classes with penalty factors.

    • For objects fitted without penalty factors this argument is not required as original data can be reconstructed from the object passed.

  • intercept: A logical value indicating whether to include the intercept.

    • The default is FALSE.

    • For the regularized models it is set to FALSE.

  • title : Custom vectors of strings specifying titles for both plots.

  • alpha : A numeric value between 0 and 1 specifying the significance level.

    • The default is 0.05.

  • palette : Custom vector of colors to highlight the direction of estimated regression coefficients or Odds Ratio.

    • Grey scale is implemented by default.

    • Values at low and high ends of the grey scale palette can be specified.

  • start : grey value at low end of palette.

    • The default value is 0.5.

  • end : grey value at high end of palette.

    • The default value is 0.9.

  • eff_size_diff : A vector specifying which values to utilize for realized effect size calculation.It is applied to all independent variables. By default it is c(4,2) which is Q3 - Q1. The following coding scheme is used:

    • 1 is the minimum.

    • 2 is the first quartile.

    • 3 is the second quartile.

    • 4 is the third quartile.

    • 5 is the maximum.

  • round_func : A string specifying how to round the realized effect size.

    • Can be either "floor", "ceiling", or "none".

    • The default value is "none".

  • glmnet_fct_var : names of categorical variables for regularized models.

    • Glmnet treats all variables as numeric.

    • If any of the variables utilized are, in fact, categorical, please, specify their name(s).

    • Please, note that that by default model.matrix()will create k-1 dummy variables in lieu of k levels of a categorical variable. For example,if you have a factor variable called "sex" with two levels 0 and 1, and 0 being the base level, mode.matrix() will create a dummy variable called "sex1". Please, utilize the names created by mode.matrix() here and not the original factor name.

  • verbose : A logical value indicating whether to display warning messages.

    • The default is FALSE.

Please note the following:

  • Only Gaussian and binomial families are currently supported.

  • Certain steps should be followed in order to produce Confidence Intervals for the regularized models. Please, refer to the vignette for the vis_reg() function and the documentation of the selectiveInference package.

  • Penalty factor of 0 is not currently supported and no Confidence Intervals will be produced in this case.

See also

Examples

# Set seed for reproducibility
set.seed(38)
# Set the number of observations
n = 1000
# Generate predictor variables
X1 = rnorm(n)
X2 = rnorm(n)
X3 = rnorm(n)
# Define coefficients for each predictor
beta_0 = -1
beta_1 = 0.5
beta_2 = -0.25
beta_3 = 0.75
# Generate the latent variable
latent_variable = beta_0 + beta_1 * X1+ beta_2 * X2 + beta_3 * X3
# convert it to probabilities
p = pnorm(latent_variable)
# Generate binomial outcomes based on these probabilities
y = rbinom(n, size = 1, prob = p)
# Fit a GLM with a probit link
glm_model <- glm(y ~ X1 + X2 + X3, family = binomial(link = "probit"),
                 data = data.frame(y, X1, X2, X3))
# Specify additional parameters and Plot Odds Ratio for the Realized Effect
vis_reg(glm_model, CI=TRUE,intercept=TRUE,
        palette=c("greenyellow","red4"))$RealizedEffectVis